Key Thoughts / Rapid Read
- After refreshing some foundational concepts, I present the most powerful procedure that I have ever encountered in science and engineering. I’m revealing the secrets that enabled me to succeed in engineering school, and in tutoring many other students along the way as well. Learn the GPS guidance system for solving problems!
- Lesson 1: Always write the units! This is the most fundamental principle for success in science (and engineering).
- Lesson 2: Math requires consistent units! Math without units is bogus, and has resulted in significant engineering disasters.
- Lesson 3: Build fractions from unit conversion factors.
- Lesson 4: Master unit conversions. Units will become your roadmap, your own GPS guidance system to solving problems!
- Lesson 5: If you ever have a problem on a test or homework and you don’t know what to do, start by writing down what you have and what you need, then “Times Line”!
- Unit Conversion in 7 Easy Steps! Do not underestimate the power of mastering this technique! At least 75% of all my tutoring in science and engineering involved drilling units and unit conversions.
- Teaser: In a follow-up post I will demonstrate how this procedure can solve seemingly complex problems in chemistry, physics and engineering with ease (even if you don’t know the theory)! Just follow the units, and they will guide you to the solution as easily as if you were navigating with a GPS. Your chemistry or physics professor might suspect you of cheating, but the proof is in the units!
Introduction
In this series on the fundamental concepts of science I’m revealing the secrets that enabled me to succeed in engineering school. These secrets also allowed me to help many others along the way, as I tutored most science and engineering courses in college. Special thanks to my high school science teacher Mrs. Frates who loves Jesus and inspired my love of science, and taught these fundamentals well.
After refreshing some foundational concepts, I present the most powerful procedure that I have ever encountered in science and engineering. We will keep it simple as we walk through this post, but in a follow-up we will demonstrate how these simple principles are applicable to everything from chemistry and physics, to engineering statics and fluid dynamics.
As an engineer I have taken many courses in various scientific disciplines, and also tutored college-level science and engineering courses. Regardless of the course, while tutoring I always went back to the basics and taught these fundamental concepts first before moving on to the specific subject. If you are in college or high school, pay especially close attention!
Concept 1 – Numbers are Meaningless in Science (and Life)
Numbers are meaningless in science, and life in general. This might sound crazy, but deep down inside you know this to be true and you act as if this is true. When confronted with a “naked” number, your brain automatically adds an assumed context, in order to interpret meaning. Consider the following statements … And before clicking (or tapping) to reveal the image, try to create your own mental image of what you expect to see. Consider what additional information you have to assume in order to add meaning to the number:
- My cousin is 7
- The snake is 7
- 1 is peeking through the fence
In order to convey meaning, all numbers must be accompanied by “Units”. Try clicking on the images again (if you haven’t already) to see what other interpretations are possible. Each number has vastly different meanings depending on the units. The difference between 7 decades old and 7 days old is huge (a lifetime of difference!), but the number is the same. I asked my 6-year-old daughter to test the above illustration by reading the sentence and then clicking … and she burst out in laughter when the 7-decade-old grandma appeared instead of the 7-year-old child that she expected. Your brain automatically must assume units in order to interpret a meaning. What did you expect to see?
One more quick example on the importance of units: Imagine you are getting hired and the recruiter offers you a salary of 300. Depending on the units this could be a very nice salary indeed, or it might leave you in poverty.
- $300/hr – Oh Yeah!
- $300/day – Above the US Average
- $300/month – Ouch!
Lesson 1: Always write the units! This is the most fundamental principle for success in science (and engineering).
Concept 2 – Math Without Units is Bogus
In 1999, NASA’s Mars Climate Orbiter mission failed when the probe was destroyed due to inconsistent units!1 Two teams of engineers designed different portions of the control systems with different units. When the space probe attempted to perform the required math, the mis-matched units resulted in bogus information that did not match reality. Thus the $125 million dollar probe missed its target and was destroyed.2
For a simple example, suppose you purchase an item for $26. Will the cashier accept a dollar bill plus a quarter? The dollar bill is worth $1, and quarter 25 cents: 1 + 25 = 26, right?
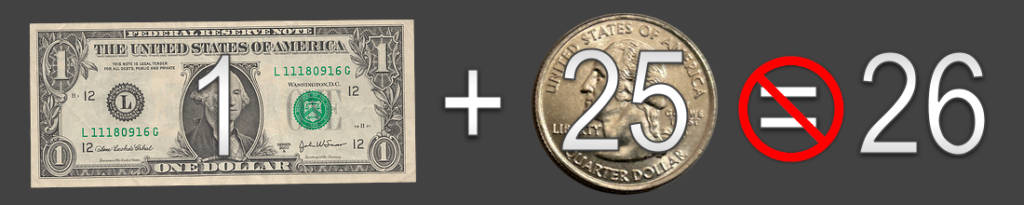
No! In order to add money the units must match! The quarter is only worth $0.25 for a combined total of $1.25, not $26!
Lesson 2: Math requires consistent units! Before doing math, all numbers must be converted into the same units.
Based on your past experience with money, the above addition of dollars and cents is likely straightforward for you. But what about other units? How do you go from inches to feet, or from miles per hour to meters per second? Before layout out the 7 Easy Steps for Unit Conversion, we we need a quick reminder about fractions:
Concept 3 – Fractions: 2 Quick Reminders, and 1 Application
Here are two quick reminders that set the groundwork for all the math that we will be using, followed by the application to unit conversion fractions. If you need a more detailed reminder on the concepts or math with fractions check out Wikipedia or your favorite reference. Otherwise, these two concepts should be fairly straightforward.
Reminder 1 – When numerator and denominator are equal, the fraction = 1
Any fraction with the same number in the numerator and denominator equals 1. For an explanation the picture is worth a thousand words. See the following illustration:
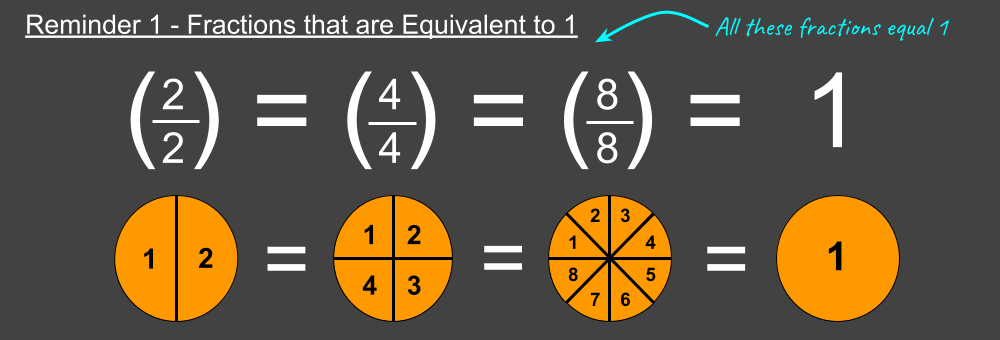
In a physical sense imagine slicing a pizza into more slices. Whether you slice it into 2, 4, or 8 pieces you alway have one pizza (until it gets eaten!).
Reminder 2 – When multiplied by a fraction equivalent to 1, the result is unchanged (just expressed differently)
In math, when any number is multiplied by 1 the number is unchanged. The same is true when multiplying by a fraction equivalent to 1 (i.e. numerator and denominator are the same):
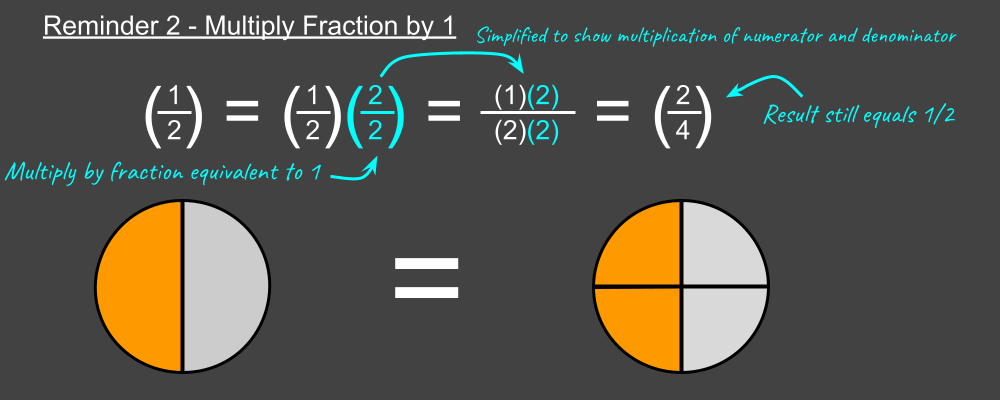
In a physical sense imagine starting with half a pizza, then slicing that half into more pieces. Whether you slice it into 2, 4, or 8 pieces it still remains half a pizza. Even though it might be expressed differently, 1/2 is the same as 2/4 is the same as 4/8.
Application to Unit Conversion Fractions
Building upon the above reminders, we apply this to unit conversions: in the same way that fractions are equal to 1 when their numerator and denominator are equal, unit conversion factors can be expressed as fractions equal to 1. We will start with a simple example converting feet to inches. The conversion factor is: 1 ft = 12 in. From this, we can build 2 fractions that equal 1, as illustrated in the following:
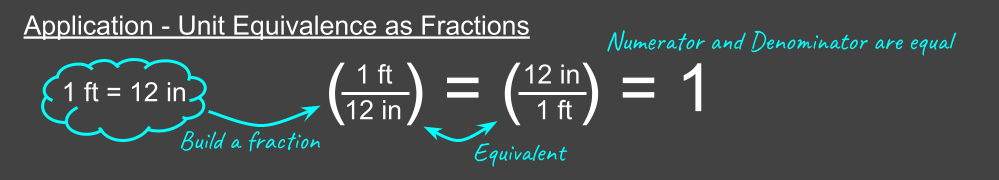
Although the expressions “1 ft” and “12 in” look totally different, in physical reality they both describe the exact same length. A pencil that is 1 ft long is exactly 12 in long. Since 1 ft = 12 in, the resulting fraction equals 1 regardless of whether feet or inches go into the numerator or the denominator.
Lesson 3: Build fractions from unit conversion factors. The resulting fractions equal 1!
But how does this help, you ask? Well … with the above background in mind, I present the most powerful procedure that I have ever encountered for solving problems in science and engineering. In just 7 easy steps you can convert ANY units. We will keep it simple as we walk through these 7 steps, but in a future post we will demonstrate how this simple procedure is applicable to everything from chemistry and physics, to engineering statics and fluid dynamics. As an engineer I use this simple procedure on-the-job nearly every day.
Concept 3 – Fractions: 2 Quick Reminders, and 1 Application
Here are two quick reminders that set the groundwork for all the math that we will be using, followed by the application to unit conversion fractions. If you need a more detailed reminder on the concepts or math with fractions check out Wikipedia3 or your favorite reference. Otherwise, these two concepts should be fairly straightforward.
Reminder 1 – When numerator and denominator are equal, the fraction = 1
Any fraction with the same number in the numerator and denominator equals 1. For an explanation the picture is worth a thousand words. See the following illustration:

In a physical sense imagine slicing a pizza into more slices. Whether you slice it into 2, 4, or 8 pieces you alway have one pizza (until it gets eaten!).
Reminder 2 – When multiplied by a fraction equivalent to 1, the result is unchanged (just expressed differently)
In math, when any number is multiplied by 1 the number is unchanged. The same is true when multiplying by a fraction equivalent to 1 (i.e. numerator and denominator are the same):
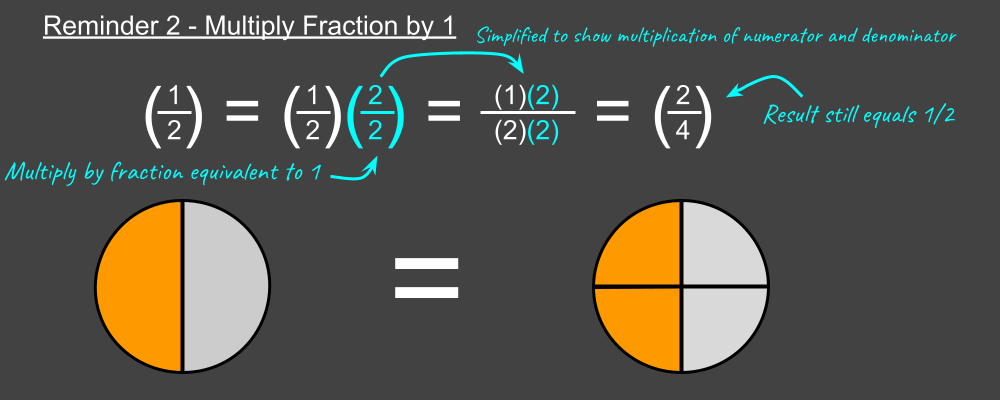
In a physical sense imagine starting with half a pizza, then slicing that half into more pieces. Whether you slice it into 2, 4, or 8 pieces it still remains half a pizza. Even though it might be expressed differently, 1/2 is the same as 2/4 is the same as 4/8.
Application to Unit Conversion Fractions
Building upon the above reminders, we apply this to unit conversions: in the same way that fractions are equal to 1 when their numerator and denominator are equal, unit conversion factors can be expressed as fractions equal to 1. We will start with a simple example converting feet to inches. The conversion factor is: 1 ft = 12 in. From this, we can build 2 fractions that equal 1, as illustrated in the following:
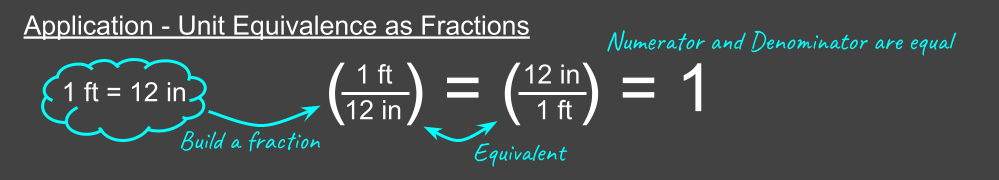
Although the expressions “1 ft” and “12 in” look totally different, in physical reality they both describe the exact same length. A pencil that is 1 ft long is exactly 12 in long. Since 1 ft = 12 in, the resulting fraction equals 1 regardless of whether feet or inches go into the numerator or the denominator.
But how does this help, you ask? Well … with the above background in mind, I present the most powerful procedure that I have ever encountered for solving problems in science and engineering. In just 7 easy steps you can convert ANY units. We will keep it simple as we walk through these 7 steps, but in a future post we will demonstrate how this simple procedure is applicable to everything from chemistry and physics, to engineering statics and fluid dynamics.
Unit Conversion in 7 Easy Steps!
Do not underestimate the power of mastering this technique! At least 75% of all my tutoring in sciences and engineering involved drilling unit conversions. If you can master unit conversions, they will become a roadmap for you, your own GPS guidance system to solving problems (and your secret “cheat sheet” on tests).
Lesson 4: Master unit conversions. Units will become your roadmap, your own GPS guidance system to solving problems!
After walking through the 7 steps below I have provided a 30-second step-by-step animation.
Step 1: “What you Have and Need”

Start by writing what you have on the left side of the paper, and what you need on the right side. The “3 ft” is where you are, “inches” is your destination, and the units will become your roadmap to get to your destination.
Step 2: “Times Line”

Add parentheses and lines to set up a multiplication of fractions. I call it “Times Line” because that is what my science teacher Mrs. Frates called it, and it is catchy and easy to remember. Whenever she did problems on the white board, she would always have us shout out “Times Line”. If you ever have a problem on a test or homework and you don’t know what to do, start by writing down what you have and what you need, then “Times Line”!!!
Step 3: “Conversion Factor”

Into the “Times Line” setup, put “1” in the denominator below what you start with, and then copy your starting units into the denominator of what will become your conversion fraction. ***Always*** copy the starting numerator units into the “times-line” denominator. Then find your conversion factor (in our example 1 ft = 12 in) and write it down.
Step 4: “Build the Fraction”

Now build the conversion fraction, using units as the roadmap. You already copied “ft” units into the denominator in Step 3, therefore put “in” units in the numerator now. Then fill in the corresponding numbers.
Step 5: “Cancel Units”

Now cancel the units, and then double check that the remaining units match what you need.. Where you have “ft” in the numerator and denominator, they cancel out. We are left with “in”, just what we need.
Step 6: “Simplify”
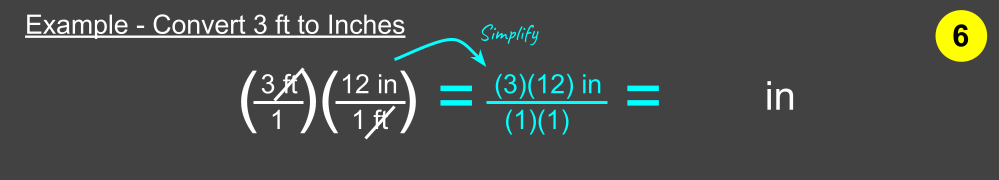
Simplify everything, careful to copy the numbers into the correct location!
Step 7: “Do the Math”
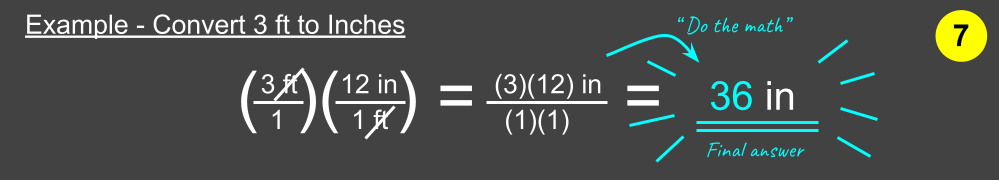
Plug the math into your calculation, and that’s it! Practice, practice, practice!
Putting it All Together

Here is an animation of all 7 steps in 30 seconds. If you ever get stuck and don’t know how to start working on a problem, just remember two simple rules: (1) Start by writing down what you have and what you need, then (2) “Times Line”! and the rest will follow.
Lesson 5: If you ever have a problem on a test or homework and you don’t know what to do, start by writing down what you have and what you need, then “Times Line”!
In a future post I will demonstrate with a series of examples to show how the exact same procedure works for complex unit conversions. I will also demonstrate how this procedure can solve seemingly complex problems in chemistry, physics, and engineering with ease (even if you don’t know the theory)! Just follow the units, and they will guide you to the solution as easily as if you were navigating with a GPS. Your chemistry or physics professor might suspect you of cheating, but the proof is in the units!